Image compression - Huffman coding

Cosine transformation together with a quantization allowed us to bring a color channel into a form where most of the data consists of only a few characters (mainly zeroes). The same can be achieved with audio files and other data, and is from the beginning given in text files (in any language). A method that can losslessly compress such data therefore has a very broad area of application.

Prefix code

Imagine the data we want to encode is 

   "13371545155135706347"

If stored as an ASCII sequence, the string would take 20 Bytes of storage. Noting that we have only eight "letters" in our "alphabet", i.e. {0,1,2,3,4,5,6,7}, a more compact way to store the string would be to use 3 Bit sequences for each letter, e.g.

numeral code
0 000
1 001
2 010
3 011
4 100
5 101
6 110
7 111

The binary encoding of the original message would be 

  001011011111001101100101001101101001011101111000110011100111
  \ /\ /\ /\ /\ /\ /\ /\ /\ /\ /\ /\ /\ /\ /\ /\ /\ /\ /\ /\ / 
   1  3  3  7  1  5  4  5  1  5  5  1  3  5  7  0  6  3  4  7

and would take up less than 8 Bytes.

In our message fives and threes occur more often than zeroes and sixes. The main idea behind entropy encoding is to use shorter codes for letters that occur often and longer codes for letters that are rare. Of course we need to be careful not to run into problems. If we for instance used 7-->0, 3-->1, 5-->01 the decoding would not be unique. 0101 could be decoded as 735 or 573 or 55 or 7373. To make the mapping uniquely invertible we need to insist that

No two codes exist in the "dictionary" where one is a prefix of the other.

In the example above 0 is a prefix of 01, so the rule is violated. Dictionaries which satisfy this rule are called prefix codes or better prefix-free codes. A prefix code for our example could be

numeral code
0 111001
1 00
2 111000
3 01
4 1111
5 10
6 11101
7 110

which would lead to the binary encoding 

  
  000101110001011111000101000011011011100111101011111110
  \/\/\/\ /\/\/\  /\/\/\/\/\/\/\/\ /\    /\   /\/\  /\ / 
  1 3 3  7 1 5  4  5 1 5 5 1 3 5  7   0     6  3  4   7

Going from left to right through the binary sequence, as soon as we recognize a letter, we are sure (due to the prefix property) that it cannot be any other letter.
0 is no code
00 is 1, and no other letter starts with 00
0 is no code
01 is 3 and no other letter starts with 01
etc.
Altogether the encoded message is 10% shorter than the original one. Depending on the data the gain can be much bigger. But of course also the dictionary needs to be stored somewhere.

Huffman coding

Huffman coding is a clever method to construct a dictionary, that is in some sense optimal for the data at hand. The method takes as input an alphabet and the probabilities with which each letter might occur in the data. The higher the probability, the shorter the code-sequence for this letter will be. I will describe how the method works, but will leave open the why. For a deeper understanding I recommend the Wikipedia entry and the original article, "A Method for the Construction of Minimum-Redundancy Codes".

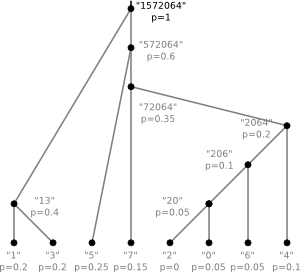
The dictionary is equivalent to a binary tree. For our example the tree would be
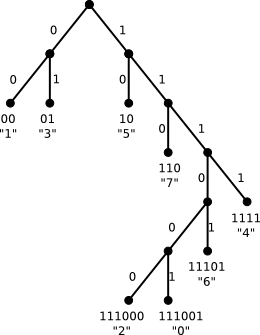
binary tree
The letters correspond to leaves and following the edges from top to bottom one can read off the code for a given letter. To construct the "optimal" tree for a given alphabet and given probabilities one follows the following algorithm:

The tree from our example was created following this algorithm with the probabilities chosen according to the number of occurrences in the string.

numeral probability
0 0.05
1 0.2
2 0
3 0.2
4 0.1
5 0.25
6 0.05
7 0.15

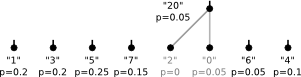
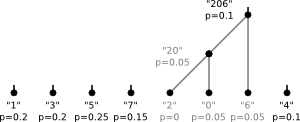
The steps of the algorithm were

1)
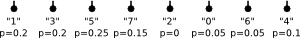
step 1

2)
step 2

3)
step 3

4)
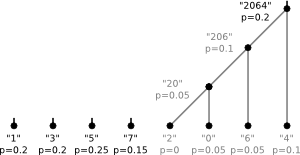
step 4

5)
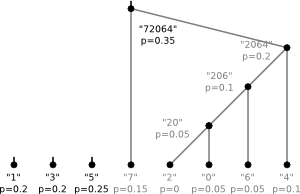
step 5

6)
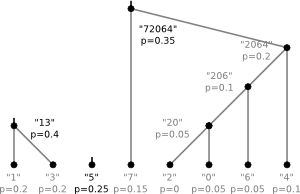
step 6

7)
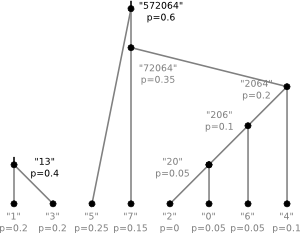
step 7

8)
step 8

Implementation

First we need a piece of code that takes an alphabet and probabilities and returns a dictionary and for later convenience also the tree. To keep the routine very general the alphabet can be a cell array. This allows the letters to be almost anything (numbers, characters, words,...). Binary trees in MATLAB are a bit problematic. Since we will not need to insert anything into an existing tree, we can abuse MATLAB's structures. Each node will be a structure, that among others has the fields zero and one, which again are structures of the same kind. In practice this could look like 

   % hufftree.m
   %
   % given alphabet and probabilities: create huffman-tree

   function [tree, table] = hufftree(alphabet,prob)

   for l=1:length(alphabet)       % create a vector of nodes (leaves), one for each letter
      leaves(l).val = alphabet{l};
      leaves(l).zero= '';
      leaves(l).one='';
      leaves(l).prob = prob(l);
   end

   % combine the two nodes with lowest probability to a new node with the summed prob.
   % repeat until only one node is left
   while length(leaves)>1                           
      [dummy,I]=sort(prob);                         
      prob = [prob(I(1))+prob(I(2)) prob(I(3:end))];
      node.zero = leaves(I(1));         
      node.one  = leaves(I(2));         
      node.prob = prob(1);
      node.val = '';
      leaves = [node leaves(I(3:end))];
   end


   % pass through the tree,
   % remove unnecessary information
   % and create table recursively (depth first)
   table.val={}; table.code={};
   [tree, table] = descend(leaves(1),table,'');


   %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
   function [tree, table] = descend(oldtree, oldtable, code)

   table = oldtable;
   if(~isempty(oldtree.val))
      tree.val = oldtree.val;
      table.val{end+1}  = oldtree.val;
      table.code{end+1} = code;
   else
      [tree0, table] = descend(oldtree.zero, table, strcat(code,'0'));
      [tree1, table] = descend(oldtree.one,  table, strcat(code,'1'));
      tree.zero=tree0;
      tree.one= tree1;
   end

The first for-loop corresponds to the first step of the algorithm. The subsequent while-loop creates the tree. When finished, the uppermost node of the tree is leaves(1). The last piece of the code translates the tree into a dictionary-table. This is realized by a recursive function that follows each branch of the tree and keeps track of how many 0-edges and 1-edges were encountered on the way.

Having the table ready, the Huffman encoding itself is very simple. Here is a function that takes the table and the input-text as parameters and returns the encoded text. 

   % huffencode.m
   %
   % takes a cell-vector and a huffman-table
   % returns a huffman encoded bit-string

   function bitstring = huffencode(input, table)

   bitstring = '';
   for l=1:length(input),
      bitstring = strcat(bitstring,table.code{strcmp(table.val,input{l})}); % omits letters that are not in alphabet
   end;

The decoding is a bit trickier - especially if one wants to avoid the comparison of each substring with the whole dictionary at each step. But of course, if we have the tree, we can just follow the branches of the tree from top to bottom according to the input, and jump back to the top once a letter is recognized. This is how the following function works 

   % huffdecode.m
   %
   % takes a bit-string and a huffman-tree
   % returns a decoded cell array

   function message = huffdecode(bitstring, tree)

   treepos = tree;
   counter = 1;
   for l=1:length(bitstring)
      if(bitstring(l) == '1')
         treepos = treepos.one;
      else
         treepos = treepos.zero;
      end
      if(isfield(treepos,'val'))
         message{counter} = treepos.val;
         counter = counter+1;
         treepos = tree;
      end
   end

To demonstrate how the pieces work together, we can repeat our example: 

   >> alphabet = {'0' '1' '2' '3' '4' '5' '6' '7'};
   >> p = [0.05 0.2 0 0.2 0.1 0.25 0.05 0.15];
   >> [tree, tab] = hufftree(alphabet,p);
   >> tab

   tab =

        val: {'1'  '3'  '5'  '7'  '2'  '0'  '6'  '4'}
       code: {'00'  '01'  '10'  '110'  '111000'  '111001'  '11101'  '1111'}

   >> message = {'1' '3' '3' '7' '1' '5' '4' '5' '1' '5' '5' '1' '3' '5' '7' '0' '6' '3' '4' '7'};
   >> code = huffencode(message,tab)

   code =

   000101110001011111000101000011011011100111101011111110

   >> decoded = huffdecode(code,tree)

   decoded =

     Columns 1 through 13

       '1'    '3'    '3'    '7'    '1'    '5'    '4'    '5'    '1'    '5'    '5'    '1'    '3'

     Columns 14 through 20

       '5'    '7'    '0'    '6'    '3'    '4'    '7'

   >>

So, everything works as expected. Maybe some last remarks: